Introduction
An "Event" is a planned gathering of masses for celebration, marketing, and education at an anticipated time and place.
Now, do you know that mathematics is used to determine the probability of the occurrence of an event or events taking place at once? Yes, probability has significantly determined the concept of events based on their distinct properties in 7 different types, viz. Simple and Compound Events, Sure and Impossible Events, Complementary, Mutually exclusive, Equally Likely, Exhaustive, Independent and Dependent Events.
However, in this article, we are going to concentrate on the difference between mutually exclusive and independent events.
Mutually Exclusive vs. Independent Events
An event is referred to as a Mutually exclusive event when the occurrence of event A interferes with the occurrence of event B, whereas an independent event occurs when event A does not distress the occurrence of event B scheduled at the same time.
- If Two sets of events, A and B, cannot appear together, then they are mutually exclusive.
- If two events can happen parallel to one another then they are independent events.
- The basic concept of mutually exclusive is often confused with independent events because both of them include two sets of events that are independent of each other.
- Independent events occur simultaneously, but only one event occurs at a time in mutually exclusive events.
- Mutually exclusive events are a little time-consuming to understand in comparison to independent events but are easier to comprehend.
Examples of the difference between Mutually Exclusive and Independent Events
A group of college students want to go camping. There are two routes; one leads to the forest and another leads to the mall. Now, which trail will they choose? They can only go in one direction. They cannot go down two different roads at the same time. Hence, this is an example of a mutually exclusive event.
A group of college students plan to spend the day together. They decide to go to a movie and later for pizza in town. Now, here, the event of going to the theater and going for some snacks after the movie is independent of each other. Hence, this is an example of an independent event.
Difference Between Mutually Exclusive and Independent Events in Tabular Form
| Mutually Exclusive Events | Independent Events |
| The case where two events do not qualify to occur simultaneously is known as a mutually exclusive event. | The case where the affair of one event does not interfere with the happening of the other is known as an independent event. |
| Only one event is possible at a time due to the influence caused by the happening of the other. | Two events are possible to occur if they do not affect one another in any way. |
| Formula: P(A ∩ B) = 0 | Formula: P(A ∩ B) = P(B) • P(A) |
| If A happens, it leads to the non-occurrence of B. | The occurrence of P(B) is not related to the event A. |
| For example, Tossing a coin would only result in either heads or tails and not both at a time. | For example., Tossing a coin resulting in heads and tossing a coin again resulting in tails are independent of each other. |
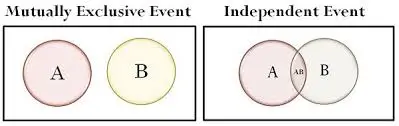
| Venn Diagram: Sets do not overlap | Venn Diagram: Sets will overlap |
What are Mutually Exclusive Events?
What do you understand about the notion of mutually exclusive events? The instances where the occurrence of two simultaneous events is not possible are referred to as Mutually Exclusive Events. Mutually exclusive events have great importance in the field of business through statistical and financial aspects. The
Mutually Exclusive Events are also popularly called Disjoint Events. The determined condition of only one event possible during an experiment is known as a disjoint event.
For example, When playing a sport, you could either win or lose.
When it is inferred that only one event has occurred in an experiment, it is concluded to be an outcome of a disjoint event. In other words, the termination of one event because of the impact of the other appearing in the same space is a mutually exclusive event.
The mathematical formula to calculate the probability of a mutually exclusive event is represented as shown below:
P (X and Y) = 0
In the situation where you choose between A and B, the outcome is collectively exhaustive as it puts off the chances of the two appearing in a recorded time. This means either A or B can only be able to take place.
For example, the result of an examination could either be a pass or a fail.
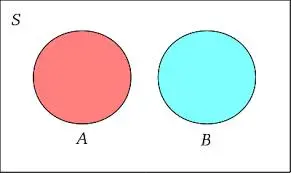
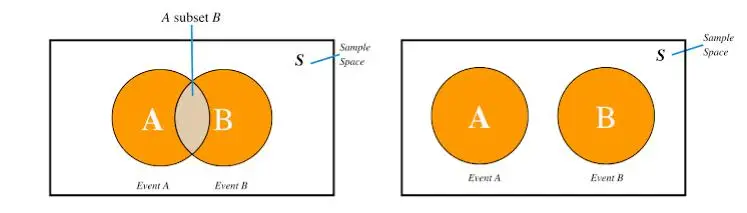
Venn's Diagram for Mutually Exclusive Events:
Here,
P is probability
P(A ∩ B) is referred to the probability of the intersection of A and B
P(A) is the probability of A
P(B) is the probability of B
The Venn diagram above shows two circles that represent two sets of independent events viz. Event A and Event B, respectively, in a given sample space. As we can see, the circles do not intersect each other, and it shows the mutual exclusivity of the events that control the outcome of either event. Hence, only one event at a time can happen in the case of mutually exclusive events.
What are Independent Events?
The instances where the occurrence of two events simultaneously does not have any impact on one another are referred to as Independent Events. Independent events are largely used for the evaluation of statistics. This means that Event A is unrelated to the occurrence of Event B simultaneously.
For example, the chances of two passengers on a bus taking a ticket to the same street stop could be used as an example of an independent event, as one passenger going to the same street does not relate to the other person getting down at the same stop.
Independent events are unaffected by past events. In other words, the occurrence of Event has no involvement whatsoever in interpreting the probability of occurrence or non-occurrence of Event Y.
The mathematical formula to calculate the probability of independent events is represented as shown below:
P (X and Y) = P(X) P(Y)
An event is termed independent when the outcome of one is not conclusive to the appearance of the other.
For example, when rolling a die, the development of the first roll is not disturbed by the development of the next roll.
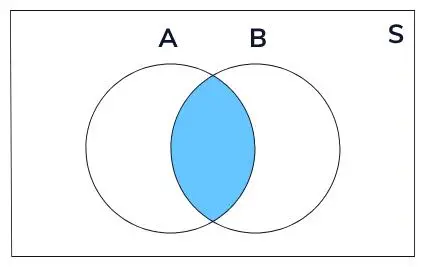
Venn's Diagram for Independent events:
Here,
P is probability
P(A ∩ B) is referred to the probability of the intersection of A and B
P(A) is the probability of A
P(B) is the probability of B
The Venn diagram above shows two circles that represent two sets of independent events viz. Event A and Event B intersect each other at a point in the middle of a given sample space. As we can see, the circles do intersect each other, and it shows that the occurrence of event A remains affected by the occurrence of event B at the same time.
Main Difference Between Mutually Exclusive Events and Independent Events in Points
- A mutually exclusive event is defined as the result of the appearance of one event canceling out the chances of the other. On the other hand, independent events are defined as two events happening at the same time without having any impact on the other.
- Mutually exclusive events do not have room for more than one event at a time. On the other hand, independent events are flexible with having two or more events at the same time without holding any control over the likelihood or the result of either event.
- In simple words, mutually exclusive events require the loss of one option for the other. At the same time, independent events allow you the opportunity to make more flexible judgments without disturbing the other.
- The mathematical formula of Mutually Exclusive Events is P(A ∩ B) = 0. The mathematical formula of Independent Events is P(A ∩ B) = P(B) • P(A)
- In Venn's diagram, the sets of mutually exclusive events do not overlap. On the contrary, in the case of independent events, the two sets of events are seen overlapping.
Conclusion
The primary difference between mutually exclusive and independent events is the situational relationship between the two sets of events. Meaning that mutually exclusive events are derived from the outcome of only one event amongst the two events occurring at a sample space. On the other hand, the occurrence of two events simultaneously without having any leverage on one another is termed an independent event.
These significant differences between the two types of probabilities are predominantly experienced in the field of business. In finance, mutual exclusivity is endured when a company has to decide between the two projects proposed to them for a new merger. Here, the selection of one is a definite rejection of the other. Similarly, for budgeting, you have an assigned budget for two bids, but naturally, you have to choose only one. You cannot choose both projects as the limitation of your budget does not allow you to do so. Hence, you are constrained to pick one over the other, and this is a statistical example of a mutually exclusive event. However, concerning independent events, the revenue obtained from one project can be used as an investment for a new project as there is no inter-relationship between the two that could disturb the statistical analysis of the projects individually.